When I was in college, it didn’t make sense to me that the position of an object on the end of a spring should be described by a function like sine or cosine, as in:
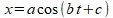
It’s just a simple harmonic oscillator. All the thing does is move back and forth. Why is there a function from trigonometry when I don’t see any circles or angles involved?
And yet our physics professor effortlessly derived it for the class on the chalkboard, and there it was. Either an integration step introduced the arcsine function into the mix, which led to sine, or a differential equation was used to directly implicate sine or cosine. I don’t recall which derivation was used that day, but both lead to trig functions. And the physics textbook[1] did the same thing. It’s as if we should just accept that there’s something subtly circular or angular about a mass on a spring. The math says so, so it must be true.
Physics was not my main focus, so I let the matter go (no pun intended). Sometime later, while looking at the integration tables in my calculus textbook[2], I reconfirmed that, yes, integrating the reciprocal of the square root of a difference of squares does in fact lead to arcsine.
So I accepted the fact that such an integral will always be tied to the shape of a circle, even if the source (e.g. a simple harmonic oscillator) has nothing to do with a circle per se. I justified that acceptance by noticing the circle-like expression in the denominator of the expression. Using different variables makes the relation more obvious.
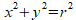
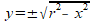
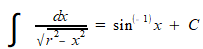
Later I was intrigued when I learned that simple harmonic oscillators were used to model some aspect of quantum physics, so I decided to review them. I found simple harmonic oscillators in my college physics book, and sure enough, those two derivations from physics class were staring back at me. One used straight integration, and the other used a differential equation. There’s that circular stuff again. But where’s the circle?
This time I was a little more observant. I noticed the similarity between the total energy equation and a circle.
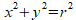
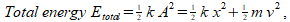where A = amplitude.
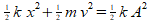
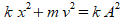
Yes, there is definitely a circle there. As the position of the mass changes, so does the velocity, and the two are constrained to a circle.
This all means that the time-dependent state of the system – particularly in terms of the position and velocity – is described by the coordinates of a circle. This is shown very well by an animated diagram in the “Simple harmonic motion” article on Wikipedia’s web site.[3] So that’s where the circle is hiding in a simple harmonic oscillator, and that’s how we get a trig function describing the position and another describing the velocity.
On a final note, it is now more clear how a richly-shaped state space involving angles and a circle can come from an object that simply moves back and forth with a linear restoring force. So it’s little surprise that chaotic behavior can come from seemingly simple situations as well.
References
[1] Sears, Francis W., Mark W. Zemansky, and Hugh D. Young. University Physics Seventh Edition. Reading, MA. Addison-Wesley Publishing Co., 1987.
[2] Anton, Howard. Calculus with Analytic Geometry. 2nd ed. New York. John Wiley & Sons, 1984.
[3] https://en.wikipedia.org/wiki/Simple_harmonic_motion
(c) Copyright 2018 by Mike Ferrell
Odd STEM 